Dominion AI Using Monte Carlo Tree Search

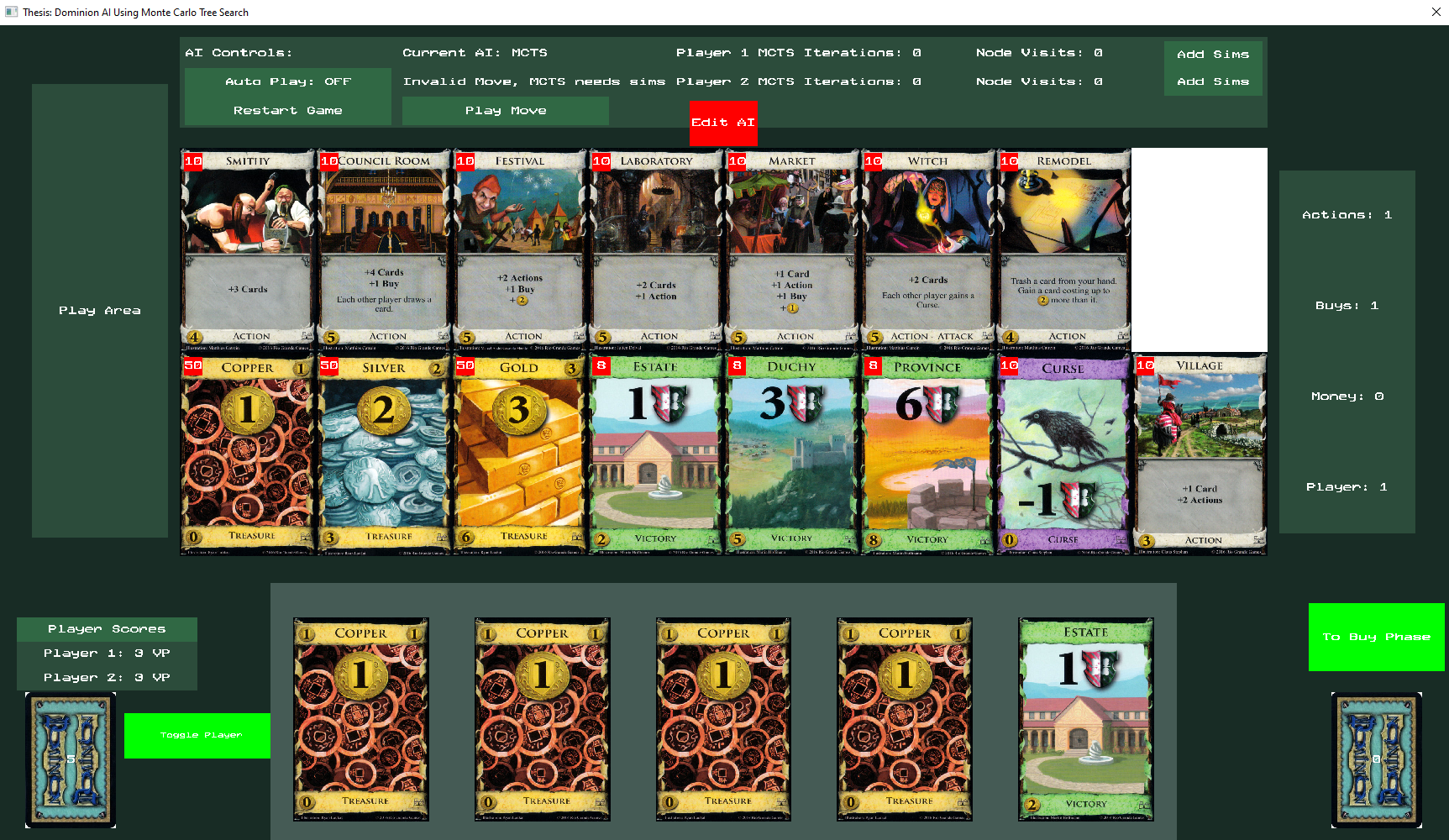
For my thesis I built the game of Dominion and an AI to play it. Keep reading to learn about both the game and the AI!

Post Mortem

What went Well

Implemented playable game of Dominion
Replaced a hotkey based UI with a fully functional and playable mouse based UI system
Handled hard problems MCTS isn’t equipped to solve like hidden information in a card game
- Don’t know what cards you will draw

What was learned

Don’t underestimate how long it will take to build the UI of a boardgame in a personal C++ engine
Implementing simple cards is easy, architecting for more complicated cards to both be playable from the UI and usable for MCTS is hard
Pivoting as new knowledge is gained is critical. Pure MCTS using random move rollouts performed atrociously, so the thesis became how to augment it to overcome hurdle and explain why pure MCTS performed so terribly

Dominion

Start of game each player:

Starts with a deck of 7 Copper and 3 Estate cards
Shuffles deck
Draws 5 cards

Anatomy of a turn:

Action Phase (Play 1 action)
Buy Phase (Buy 1 card from set of piles)
Cleanup Phase (End turn, discard hand, draw 5)

Anatomy of a card

Card Effect

What you gain when you play the card

Card Type

Action, Victory, or Treasure

Card Cost

Cost to buy

Implementation of a Gamestate

Playerboard

A Playerboard is made up of a player’s hand, play area, discard pile and deck. These are stored in a terribly named container class “cardPile” which is an array of the count of each card. I only realized how terrible when writing this here. Storing only the counts allows us to ignore the order of cards for the hand, play area, and discard pile which is great in later use by MCTS when we will need to compare game states and order of the hand doesn’t matter. The order of the deck does matter, so it is stored in a vector.

Gamestate

All game data is stored in the Gamestate and contains:

Both player’s playerboards
Current card piles
Whose turn
Current phase of player’s turn

struct gamestate_t
{
public:
	//Card Piles depicting what cards are in the game and how many are in that pile
	std::array< pileData_t, NUMBEROFPILES > m_cardPiles{};

	PlayerBoard m_playerBoards[2];
	int m_whoseMoveIsIt = PLAYER_1;
	eGamePhase m_currentPhase = CLEANUP_PHASE;
	bool m_isFirstMove = false;

public:
	gamestate_t() = default;
	gamestate_t( gamestate_t const& copyGameState ) :
		m_whoseMoveIsIt( copyGameState.m_whoseMoveIsIt ),
		m_currentPhase( copyGameState.m_currentPhase ),
		m_isFirstMove( copyGameState.m_isFirstMove )
	{
		m_playerBoards[0] = copyGameState.m_playerBoards[0];
		m_playerBoards[1] = copyGameState.m_playerBoards[1];
		memcpy( &m_cardPiles[0], ©GameState.m_cardPiles[0], NUMBEROFPILES * sizeof(pileData_t) );
	}
	gamestate_t( pileData_t gamePiles[NUMBEROFPILES], PlayerBoard const& player1Deck, PlayerBoard const& player2Deck, int whoseMove, eGamePhase const& currentPhase ) :
		m_whoseMoveIsIt( whoseMove ), m_currentPhase( currentPhase )
	{
		m_playerBoards[0] = player1Deck;
		m_playerBoards[1] = player2Deck;
		memcpy( &m_cardPiles[0], gamePiles, NUMBEROFPILES * sizeof(pileData_t) );
	}

	void ResetDecks()
	{
		m_playerBoards[0].ResetBoard();
		m_playerBoards[1].ResetBoard();
	}

	void ShuffleDecks()
	{
		m_playerBoards[0].ShuffleDeck();
		m_playerBoards[1].ShuffleDeck();
	}

	//MCTS needs a compare where order doesn't matter
	//Because we don't know what the opponent has in their hand and deck we only compare the current player
	bool UnordereredEqualsOnlyCurrentPlayer( gamestate_t const& compare ) const
	{
		if( m_whoseMoveIsIt == compare.m_whoseMoveIsIt &&
			m_currentPhase == compare.m_currentPhase )
		{
			bool playerCompare = m_playerBoards[m_whoseMoveIsIt].UnorderedCompare( compare.m_playerBoards[m_whoseMoveIsIt] );
			bool pileCompare = (m_cardPiles == compare.m_cardPiles);

			return playerCompare && pileCompare;
		}

		return false;
	}

	int WhoJustMoved()
	{
		if( m_currentPhase == ACTION_PHASE )
		{
			if( m_whoseMoveIsIt == PLAYER_1 )
			{
				return PLAYER_2;
			}
			else
			{
				return PLAYER_1;
			}
		}
		else
		{
			return m_whoseMoveIsIt;
		}
	}

	PlayerBoard& GetEditableCurrentPlayerBoard()
	{
		return m_playerBoards[m_whoseMoveIsIt];
	}
	PlayerBoard const& GetCurrentPlayerBoard()
	{
		return m_playerBoards[m_whoseMoveIsIt];
	}

	static gamestate_t ParseGameStateFromBuffer( byte*& buffer )
	{
		gamestate_t gameState;

		for( pileData_t& pileData : gameState.m_cardPiles )
		{
			pileData = pileData_t::ParsePileDataFromBuffer( buffer );
		}

		gameState.m_playerBoards[0] = PlayerBoard::ParsePlayerBoardFromBuffer( buffer );
		gameState.m_playerBoards[1] = PlayerBoard::ParsePlayerBoardFromBuffer( buffer );
		
		gameState.m_whoseMoveIsIt = ParseInt( buffer );
		
		gameState.m_currentPhase = *(eGamePhase*)buffer;
		buffer += sizeof(gameState.m_currentPhase);

		gameState.m_isFirstMove = ParseBool( buffer );

		return gameState;
	}

	//Saving and loading of the gamestate
	static gamestate_t ParseGameStateFromBufferParser( BufferParser& bufferParser )
	{
		gamestate_t gameState;

		for( pileData_t& pileData : gameState.m_cardPiles )
		{
			pileData = pileData_t::ParsePileDataFromBufferParser( bufferParser );
		}

		gameState.m_playerBoards[0] = PlayerBoard::ParsePlayerBoardFromBufferParser( bufferParser );
		gameState.m_playerBoards[1] = PlayerBoard::ParsePlayerBoardFromBufferParser( bufferParser );

		gameState.m_whoseMoveIsIt = bufferParser.ParseInt32();
		gameState.m_currentPhase = (eGamePhase)bufferParser.ParseInt32();
		gameState.m_isFirstMove = bufferParser.ParseBool();

		return gameState;
	}

	void AppendGameStateToBuffer( std::vector& buffer, size_t& startIndex ) const
	{
		for( pileData_t pileData : m_cardPiles )
		{
			pileData.AppendPileDataToBuffer( buffer, startIndex );
		}

		m_playerBoards[0].AppendPlayerBoardToBuffer( buffer, startIndex );
		m_playerBoards[1].AppendPlayerBoardToBuffer( buffer, startIndex );
		AppendDataToBuffer( (byte*)&m_whoseMoveIsIt, sizeof(m_whoseMoveIsIt), buffer, startIndex );
		AppendDataToBuffer( (byte*)&m_currentPhase, sizeof(m_currentPhase), buffer, startIndex );
		AppendDataToBuffer( (byte*)&m_isFirstMove, sizeof(m_isFirstMove), buffer, startIndex );
	}

	void AppendGameStateToBufferWriter( BufferWriter& bufferWriter ) const 
	{
		for( pileData_t pileData : m_cardPiles )
		{
			pileData.AppendPileDataToBufferWriter( bufferWriter );
		}

		m_playerBoards[0].AppendPlayerBoardToBufferWriter( bufferWriter );
		m_playerBoards[1].AppendPlayerBoardToBufferWriter( bufferWriter );
		bufferWriter.AppendInt32( m_whoseMoveIsIt );
		bufferWriter.AppendInt32( m_currentPhase );
		bufferWriter.AppendBool( m_isFirstMove );
	}
};
    
    

class PlayerBoard
{
public:
	PlayerBoard();
	~PlayerBoard() = default;

	//Mutators
	void InitializeDeck( std::vector& deck );
	void ResetBoard();

	void PlayCard( inputMove_t const& inputMove, gamestate_t* gameState );
	void ShuffleDeck();
	void DiscardHand();
	void Draw( int numberToDraw = 1 );
	void Draw5();
	void PlayTreasureCards();
	void DiscardPlayArea();
	void AddCardToDiscardPile( int cardIndex );
	void AddDiscardPileToDeck();
	void TakeCardFromHand( size_t cardIndex );
	void DecrementCoins( int cost ) { m_currentCoins -= cost; }
	void ResetCurrentCoins() { m_currentCoins = 0; }
	void RandomizeHandAndDeck();

	//Accessors
	bool CanPlayCard( inputMove_t const& inputMove, gamestate_t const* gameState ) const;
	
	CardPile const& GetHand() const;
	CardPile const& GetPlayArea() const;

	int GetCurrentMoney() const { return m_currentCoins; }
	int GetCurrentVictoryPoints() const;
	size_t GetDeckSize() { return m_deck.size(); }
	size_t GetDiscardSize() { return (size_t)m_discardPile.TotalCount(); }
	int GetNumberOfValidSimpleActionsToPlay() const;
	bool UnorderedCompare( PlayerBoard const& compare ) const;
	bool HasCard( int cardIndex ) const;
	int GetCardIndexFromHandIndex( int handIndex );
	int GetCountOfCard( int cardIndex ) const;

	//Saving and loading to file
	void AppendPlayerBoardToBuffer( std::vector& buffer, size_t& startIndex ) const;
	void AppendPlayerBoardToBufferWriter( BufferWriter& bufferWriter ) const;
	void ParseFromBuffer( byte*& buffer );
	void ParseFromBufferParser( BufferParser& bufferParser );
	static PlayerBoard ParsePlayerBoardFromBuffer( byte*& buffer );
	static PlayerBoard ParsePlayerBoardFromBufferParser( BufferParser& bufferParser );

private:
	void AddHandToDeck();
public:

	CardPile m_hand;
	CardPile m_discardPile;
	CardPile m_playArea;
	CardPile m_sortedDeck;
	int m_currentCoins = 0;
	int m_numberOfActionsAvailable = 1;
	int m_numberOfBuysAvailable = 1;
private:
	std::vector m_deck;
};

Implementation of a card

Card Definition

CardDefinition stores all of the data for each card. Any “complicated” card actions like the witch that gives opponents curses is stored as a boolean of “doesGiveOpponentsCurse” or similar.

Playing a card

PlayerBoard::PlayCard is the bread and butter of the game. This method will play the card and update gamestate. Here is where I learned of a weakness of my implementation. Simple cards the add actions or buys are easy, but if the card does more complicated things this method will get messy fast as well as its sister method CanPlayMove();

void PlayerBoard::PlayCard( inputMove_t const& inputMove, gamestate_t* gameState )
{
	int handIndex = inputMove.m_cardIndex;
	if( m_hand[handIndex] <= 0 )
	{
		return;
	}

	CardDefinition const* cardToPlay = CardDefinition::GetCardDefinitionByType( (eCards)handIndex );
	if( cardToPlay->GetCardType() == ACTION_TYPE )
	{
		if( gameState )
		{
			//Move card to play area
			m_hand.RemoveCard( (int)handIndex );
			m_playArea.AddCard( (int)handIndex );

			int actionsToGain = cardToPlay->m_actionsGained;
			int cardDraw = cardToPlay->m_cardDraw;
			int buysToGain = cardToPlay->m_buysGained;
			int coinsToGain = cardToPlay->m_coins;

			m_numberOfActionsAvailable += actionsToGain;
			m_numberOfBuysAvailable += buysToGain;
			m_currentCoins += coinsToGain;
			Draw( cardDraw );

			if( cardToPlay->m_OpponentsDrawCard )
			{
				PlayerBoard* player1Deck = &gameState->m_playerBoards[0];
				PlayerBoard* player2Deck = &gameState->m_playerBoards[1];

				if( player1Deck != this )
				{
					player1Deck->Draw();
				}
				else if( player2Deck != this )
				{
					player2Deck->Draw();
				}
			}

			//Witch Card
			if( cardToPlay->m_OpponentsGetCurse )
			{
				PlayerBoard* player1Deck = &gameState->m_playerBoards[0];
				PlayerBoard* player2Deck = &gameState->m_playerBoards[1];

				if( player1Deck != this )
				{
					pileData_t& pileData = gameState->m_cardPiles[(int)CURSE];
					if( pileData.m_pileSize > 0 )
					{
						pileData.m_pileSize -= 1;
						player1Deck->m_discardPile.AddCard( CURSE );
					}
				}
				if( player2Deck != this )
				{
					pileData_t& pileData = gameState->m_cardPiles[(int)CURSE];
					if( pileData.m_pileSize > 0 )
					{
						pileData.m_pileSize -= 1;
						player2Deck->m_discardPile.AddCard( CURSE );
					}
				}
			}
		}
		else
		{
			ERROR_AND_DIE("Gamestate is required for a action card to be played");
		}
	}
}

class CardDefinition
{
public:
	CardDefinition() = delete;
	CardDefinition( int cardIndex, eCardType type, std::string cardName, Texture const* cardTexture = nullptr, int cost = 0, int coins = 0, int vp = 0, int plusActions = 0, int plusDraw = 0, int plusBuys = 0 );
	~CardDefinition() {}

	static void InitializeCards();
	static CardDefinition const* GetCardDefinitionByType( eCards cardType );
	static std::vector s_definitions;

	static bool UnorderedCompare( std::vector const& first, std::vector const& second );

	int GetCardIndex() const { return m_cardIndex; }
	int GetCardCost() const { return m_cost; }
	int GetCoins() const { return m_coins; }
	eCardType GetCardType() const { return m_type; }
	int GetCardVPs() const	{ return m_victoryPointValue; }
	std::string const& GetCardName() const { return m_cardName; }
	Texture const* GetCardTexture() const { return m_cardTexture; }

public:
	int m_cardIndex = -1;
	int m_cost = -1;
	eCardType m_type = InvalidType;
	int m_coins = -1;
	std::string m_cardName;
	int m_victoryPointValue = 0;
	int m_actionsGained = 0;
	int m_cardDraw = 0;
	int m_buysGained = 0;
	Texture const* m_cardTexture = nullptr;


	bool m_OpponentsGetCurse = false;
	bool m_OpponentsDrawCard = false;
	bool m_trashUpToFourCards = false;
	bool m_discardUptoHandSizeToDrawThatMany = false;
	bool m_trashCardFromHandToGainCardOfValue2Higher = false;
};

Implementation of a UI System

Widget

The UI System depends on the Widget. It uses a transform hierarchy to stay relative to its parent widgets. The transform hierarchy is overkill because it is 3D, but I understood it well after using a similar system to implement skeletal meshes. It is used both for getting the world position and dimensions but also for checking mouse over

Render

  Mat44 Widget::GetRelativeModelMatrixScaleOnlySelf() const
{
	Mat44 parentRelativeMatrixNoScale;
	if( m_parentWidget )
	{
		parentRelativeMatrixNoScale = m_parentWidget->GetParentRelativeModelMatrixNoScale();
	}

	Mat44 myLocalMatrix = m_widgetTransform.ToMatrix();

	parentRelativeMatrixNoScale.TransformBy( myLocalMatrix );
	return parentRelativeMatrixNoScale;
}

void Widget::Render()
{
	if( !m_isEnabled )
	{
		return;
	}

	//Render Self
	if( nullptr != m_mesh && m_isVisible )
	{
		RenderContext* context = m_mesh->m_renderContext;
		if( nullptr != context )
		{
			//Ignore parent's scale, so we can think about the scale as the actual dimensions
			Mat44 modelMatrix = GetRelativeModelMatrixScaleOnlySelf();

			context->SetModelMatrix( modelMatrix );
			context->BindShader( (Shader*)nullptr );

			if( m_isSelected )
			{
				context->BindTexture( m_selectedTexture );
				context->DrawMesh( m_mesh );
			}
			else if( m_isHovered )
			{
				context->BindTexture( m_highlightTexture );
				context->DrawMesh( m_mesh );
			}
			else
			{
				context->BindTexture( m_texture );
				context->DrawMesh( m_mesh );
			}

			if( m_text.size() > 0 )
			{
				Mat44 textModelMatrix = GetRelativeModelMatrixNoScale();
				context->SetModelMatrix( textModelMatrix );
				AABB2 textBox = GetLocalAABB2();
				context->DrawAlignedTextAtPosition( m_text.c_str(), textBox, m_textSize, m_textAlignent );

			}
		}
	}

	//Render Children on top of self
	for( Widget* childWidget : m_childWidgets )
	{
		if( nullptr != childWidget )
		{
			childWidget->Render();
		}
	}
}

Monte Carlo Tree Search

MCTS tries to make the strongest AI possible. To understand how it works we should first look at the pros and cons of other methods.

Other AI strategies (State machine, Genetic Algorithm, Portfolio Search, etc. )

Use a common AI strategy to solve a specific problem

Cons

Must make a new AI for every game
Most likely won’t handle every specific case for a complicated game

Pros

Always gives an answer
Can tune for a specific game

Using a Tree

Build a tree of all possible moves and use it to decide which move has the highest chance of a win

Cons

Won’t give an answer until tree is fully built
Takes too long to build a complete tree for most games

Pros

Complete tree always gives perfect answer
Can be theoretically used on any game

Goal: Combine benefits of tree with an AI strategy

How?

If we play an AI strategy from a winning position we’d trust the AI more than from a neutral position.

Deciding what is a winning position is difficult, but playing an game using the same AI strategy for both players will give us a rough estimate.
If we build a tree of depth 5, play games using our AI strategy, and record results we can decide which move gets us to the highest winning position according to the AI used.
If we go to depth 10, 20, or more we can trust our results even more.
If we keep mapping until all possible moves are reached we’ve transitioned to a complete tree search

Using Random moves as our AI strategy for pure MCTS

Random moves is worse than a smarter AI strategy, but if the tree is big enough we can trust in the law of large numbers to decide that a move leads to a winning position

Use random moves to build the tree

At any point you should be able to ask the tree what is the best move

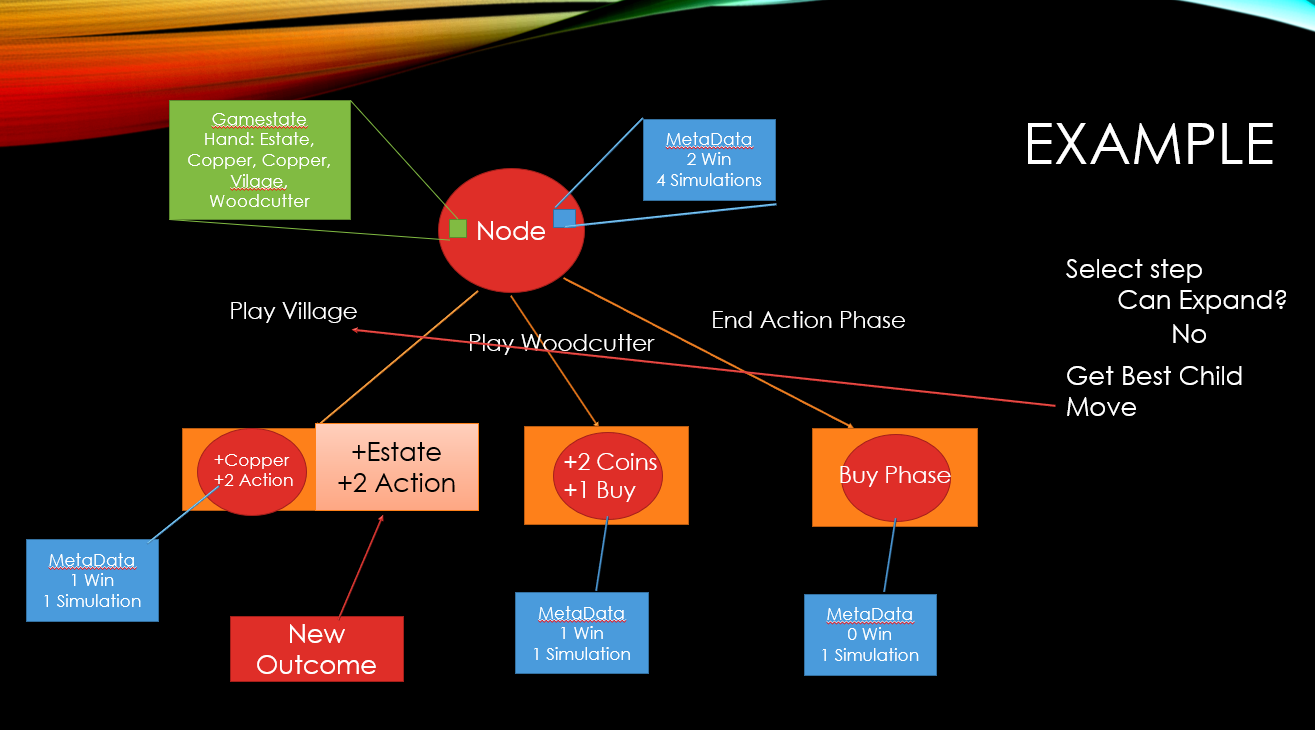
Steps to build the tree

Select
Expand
Rollout
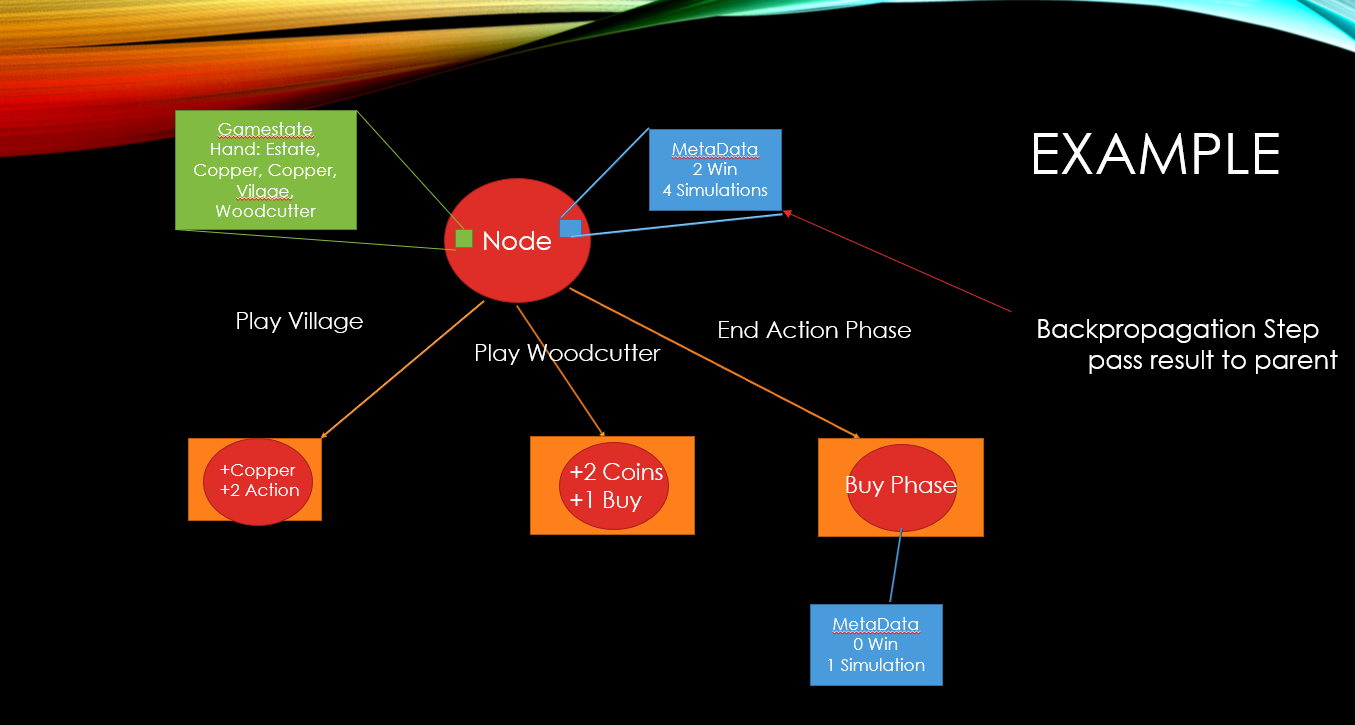
Backpropagation

Score= Winrate, C theoretically equals Sqrt(2)UCT tries to balance going deep in the tree following highest score versus going wide in the tree following exploration value. The exploration value is ~0-1 with its weight being determined by C. C can b… — Score= Winrate, C theoretically equals Sqrt(2)
UCT tries to balance going deep in the tree following highest score versus going wide in the tree following exploration value. The exploration value is ~0-1 with its weight being determined by C. C can be changed depending on what the AI programmer wants.

Select best node to expand

Can I expand the current node? Yes, move to expand step
If no, ask children which is best node
Best node is calculated using Upper Confidence Bounds Applied To Trees (UCT) formula

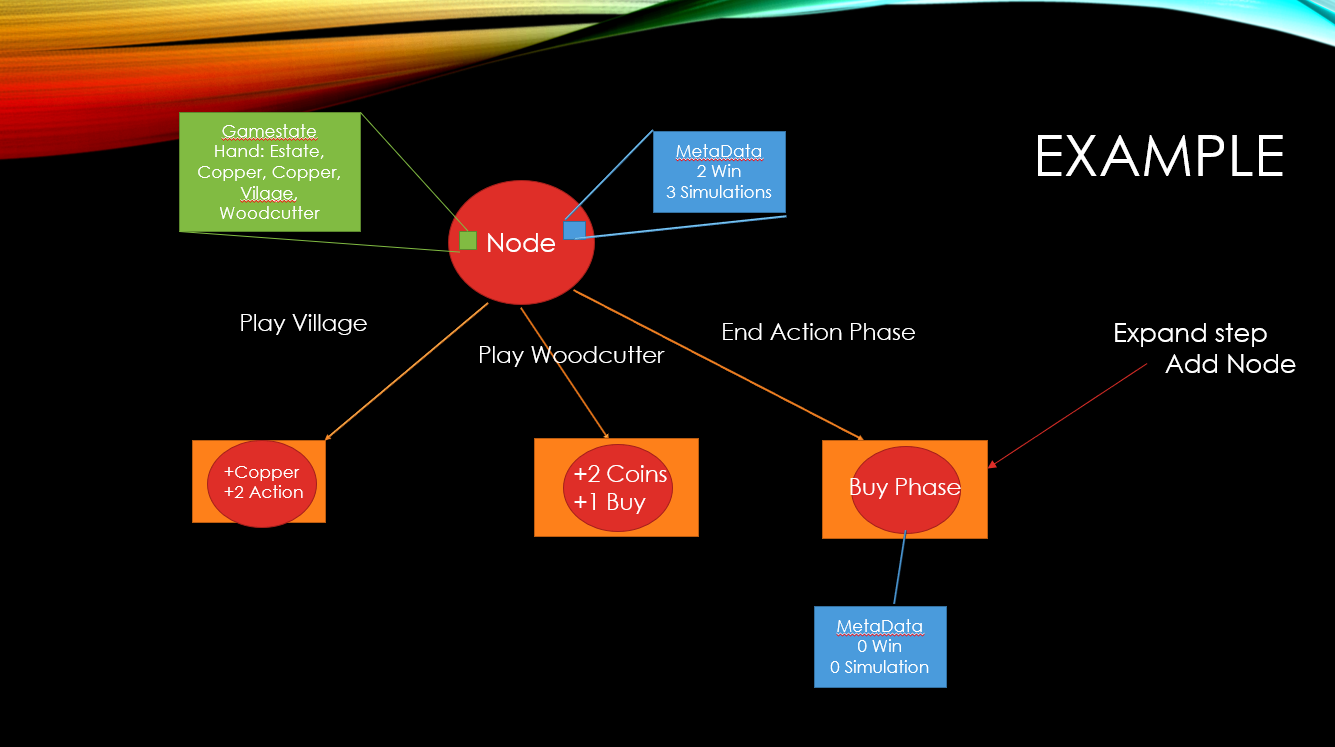
Expand (Add node to tree at selected node)

Add a move that hasn’t been added to selected node’s gamestate

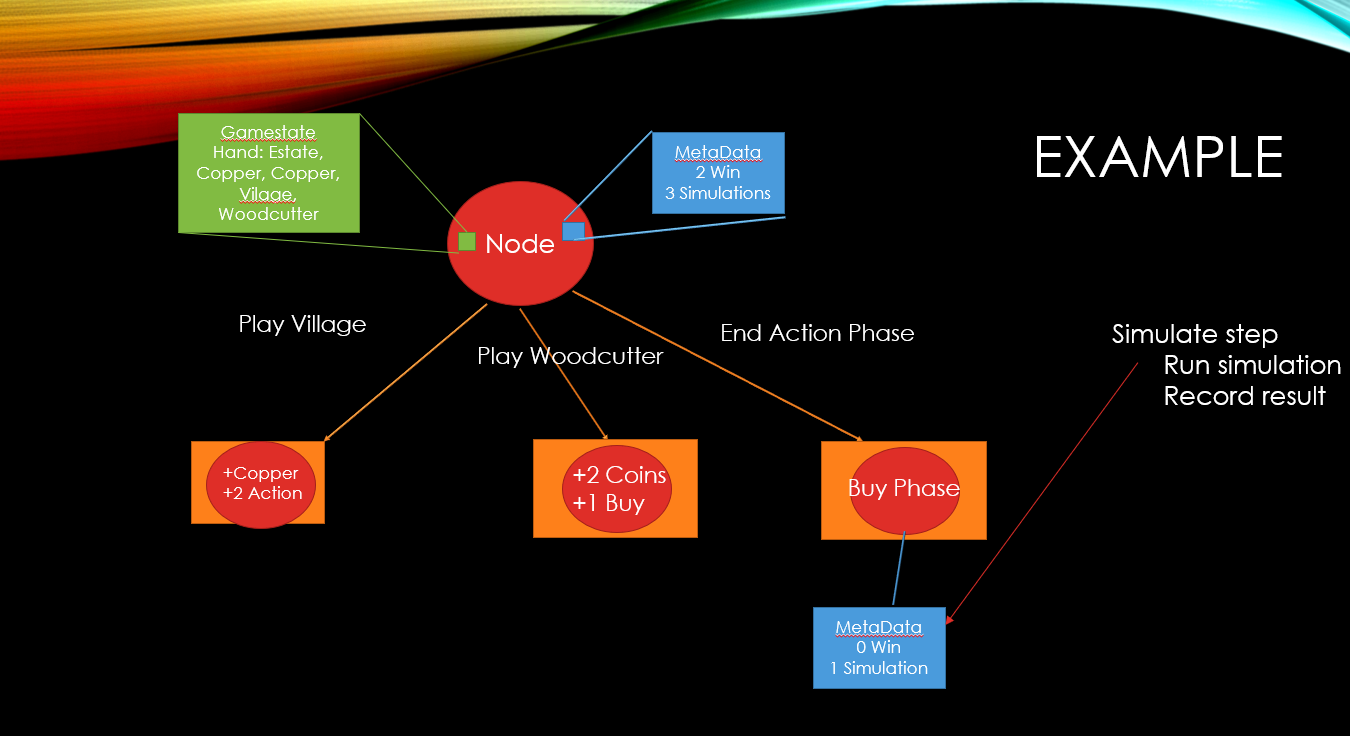
Rollout (run a simulation with specified AI)

Play a game using the specified AI for both players
1. Pure MCTS uses random moves as the AI to make it general to any problem
Return result of win, loss, or tie as 1, 0, or 0.5

Backpropagation

Return result up tree keeping relative to current player

Implementation of Monte Carlo Tree Search for Dominion

Problem:

Hidden information like what cards you will draw and what your opponent has in his/her hand mean a move could lead to multiple possible outcomes

Solution:

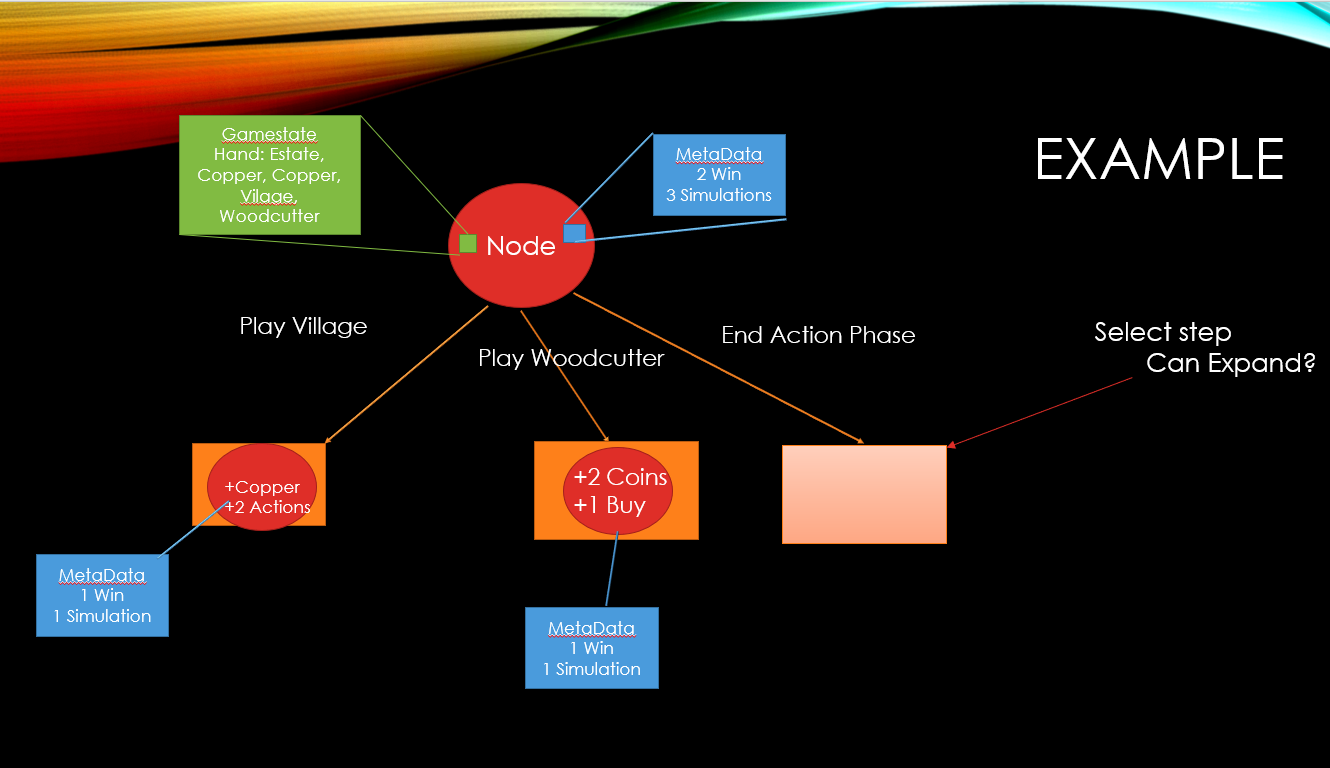
At any node in the tree, each child move now contains a list of possible outcomes.
Select step is modified to ask the game for a random outcome when a move is played to decide if it should be adding a new outcome to the best selected move or if it should continue down the tree.
- Critical to have method for comparing game states

Example:

Given hand displayed

Current Phase: Action
- Play Village
- Play Woodcutter
- End Action Phase

Problem:

Pure MCTS using random move rollouts performs poorly against simple state machine AIs

Context: Random move rollouts performs poorly because random moves end games by emptying three piles. Most strong Dominion strategies end by emptying the Province card pile. Also random moves doesn’t know how to play cards in order. If one card gives extra actions and another draws you cards, playing the draw card first means you cannot play the one to give extra actions. This means buying the card that gives actions looks worse than it actually is.

Solution: Add some expert knowledge by using a simple state machine AI instead of using random moves.

Dominion AI Using Monte Carlo Tree Search

For my thesis I built the game of Dominion and an AI to play it. Keep reading to learn about both the game and the AI!

Post Mortem

What went Well

What was learned

Dominion

Dominion is a deckbuilding game of 2 to 4 players where each player takes turns playing and buying cards from a set of card piles

Anatomy of a turn:

Anatomy of a card

Implementation of a Gamestate

Playerboard

Gamestate

Implementation of a card

Card Definition

Playing a card

Implementation of a UI System

Widget

Render

Monte Carlo Tree Search

Other AI strategies (State machine, Genetic Algorithm, Portfolio Search, etc. )

Using a Tree

Goal: Combine benefits of tree with an AI strategy

How?

Steps to build the tree

Select

Expand

Rollout

Backpropagation

Select best node to expand

Implementation of Monte Carlo Tree Search for Dominion

Problem:

Hidden information like what cards you will draw and what your opponent has in his/her hand mean a move could lead to multiple possible outcomes

Problem:

Pure MCTS using random move rollouts performs poorly against simple state machine AIs